Esta semana de vacaciones he comenzado con la lectura del libro El camino a la realidad del matemático y físico Roger Penrose, y lo cierto es que pinta interesante, aunque a priori el grosor del ejemplar produce cierta desazón. En el primer capítulo habla sobre la necesaria y escurridiza idea de la verdad matemática. Tras una primera lectura, todavía tengo muy desordenadas las ideas sobre ello en mi cabeza. Sirva esta anotación para ir aclarándolas, con vuestra ayuda, si os parece.
Parece obvio que en nuestro afán por conocer el mundo se hace indispensable desde un primer momento separar lo verdadero de lo hipotético —y esto nos conduce a una pregunta todavía más polémica: ¿existe la verdad?—, y esta función es cumplimentada con una extraordinaria precisión gracias a una herramienta tan poderosa como las matemáticas. Gracias al mundo de las matemáticas, somos capaces de abstraer e idealizar el mundo físico y describir con increíble precisión las leyes que lo gobiernan.
Ahora bien, ¿existen las matemáticas? ¿Dónde está el «mundo» de las matemáticas? De alguna manera parece estar separado del mundo físico, ya que un círculo dibujado en la arena, o con gran precisión en la pantalla de un ordenador, jamás alcanzará la perfección de la idea matemática de círculo. Desde luego, las matemáticas existen, pero parece que hay que ampliar un poco este concepto de «existencia» que tenemos. ¿Existencia mental, tal vez? ¿Las matemáticas son un producto de nuestro cerebro? Cualquiera que haya pasado unos minutos fascinado por un desarrollo matemático más o menos complejo, se habrá sentido como un mero explorador, un simple caminante llevado por la lógica a través de un paisaje que siempre ha estado ahí. Tomemos como ejemplo el famoso conjunto de Mandelbrot. Cuando Benoît Mandelbrot comenzó a investigar esta sencillísima fómula matemática y empezó a vislumbrar la forma que toma, seguro que no se imaginó la fascinante complejidad que alcanza en todos sus detalles. ¡Es algo inabarcable para la mente humana!, por lo que no parece una creación de esta. Por otra parte, antes de la existencia de ninguna forma de vida, e incluso después de esta (si se exitinguiese por completo alguna vez), está claro que el universo estuvo y seguirá regido por las mismas leyes matemáticas que hoy desentrañamos con nuestra capacidad cognitiva.
Así pues, las matemáticas son algo intemporal, y la verdad matemática se corresponde con la verdad objetiva, consituyendo la única herramienta capaz de ayudarnos a extraer conocimiento objetivable de la realidad que nos rodea. También hemos llegado a la conclusión de que las matemáticas existen de alguna manera por sí mismas fuera de nosotros, pero esta existencia no se corresponde con el significado físico habitual al que estamos acostumbrados. Roger Penrose separa la «existencia» matemática de la «existencia» física y la mental, y se refiere a la primera de forma metafórica como el «mundo matemático-platónico». Tres tipos de existencia, tres mundos misteriosamente interconectados entre sí.
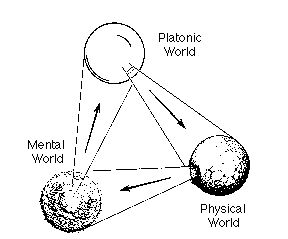
¿Tres mundos, o un todo del que tenemos muy poca idea? Después de todo, el mundo matemático se nos revela íntimamente ligado al mundo físico, tal vez sólo sea una propiedad intrínseca de este. Y dado que el cerebro —capaz de procesar las propiedades físicas que los sentidos son capaces de percibir y hacerle llegar— está compuesto de materia y por lo tanto sigue esas leyes, es lógico que un ser vivo sea a su vez capaz de llegar a percibir esta propiedad matemática de la realidad. Todos los seres vivos tenemos alguna capacidad en este sentido. El pez arquero desentraña sin saberlo diversas leyes para cazar a su presa. El ser humano, además, tiene la capacidad de abstraerlas y formularlas en un lenguaje matemático. Lo curioso de nuestra capacidad de abstracción es que nos permite desarrollar este lenguaje hasta llegar a verdades matemáticas que en apariencia nada tienen que ver con la realidad (aunque a veces nos vemos sorprendemos con aplicaciones inesperadas).
En fin, ya os he dicho que andaba con las ideas un poco desordenadas. Seguiremos leyendo y más adelante tal vez vuelva sobre este y otros temas.

