El dodecafonismo es una técnica compositiva ideada por Arnold Schönberg a principios del siglo XX como una evolución natural de la música tonal, o al menos lógica. El Romanticismo y el Postromanticismo alemán, de la mano de compositores como Wagner y Mahler, habían llevado el sistema tonal hasta sus últimas consecuencias añadiendo cada vez más tensiones, más disonancias. De entre las corrientes que surgieron a finales del siglo XIX y principios del XX que reaccionaban contra todo lo anterior (contra la música tonal, por tanto), aparece la música atonal enmarcada dentro de la corriente estética del Expresionismo. El sistema atonal pretende ser lo contrario del sistema tonal: ningún sonido es más importante que otro y además no pueden combinarse de ninguna manera que recuerde a la tonalidad. Schönberg hablaba de «la democracia de los sonidos». Y el dodecafonismo surge como una técnica, una metodología, para hacer música atonal.
Para componer una obra dodecafónica, el primer paso es escoger una serie con la que trabajar. Una serie dodecafónica es una ordenación de los doce sonidos del sistema temperado (Do, Do#, Re, Re#, Mi, Fa, Fa#, Sol, Sol#, La, La#, Si) sin repeticiones; es decir, una permutación de estas doce notas. En los libros de teoría musical suele decirse que las series constituyen un material casi inagotable, puesto que pueden formarse unas 500 millones. Está clara la cuenta que han hecho: permutaciones de 12 elementos, 12! = 479 001 600 series. Sin embargo, las reglas del dodecafonismo (mucho más estrictas que las «ataduras» del sistema tonal de las que se pretendía huir) nos reducen bastante la cantidad final disponible. Concretamente, para el que tenga prisa por saber la solución (el resto que siga leyendo), el material total asciende a:

Siguen siendo un buen puñado, pero desde luego ya no parecen «inacabables», y más teniendo en cuenta que se evitaban las progresiones que sonasen «tonales» (como Do-Mi-Sol, por ejemplo), así que de esos 10 millones realmente habría que quitar muchas más.
¿Cómo hemos sacado la cuenta? Antes que nada, para aclararnos mejor a partir de ahora, vamos a identificar cada nota con un número (o con una letra cuando se nos acaben los números), a saber: 0123456789AB. En primer lugar, hay que conocer un par de reglas fundamentales:
- Los once transportes posibles de una serie se consideran el mismo material. Transportar una serie consiste en sumarle a todas las notas un número de semitonos constante. Por ejemplo, {0123456789AB} + 1 = {123456789AB0} (perdonadme por esta notación improvisada). Es de recibo, por tanto, dividir entre doce esos casi 500 millones iniciales.
- Cada serie tiene 3 derivadas que se consideran el mismo material: la inversión, la retrogradación, y la retrogradación de la inversión. I, R y RI respectivamente a partir de ahora. La I consiste en invertir el sentido de la serie (para {0123456789AB}, I = {0BA987654321}); la R consiste en leerla de atrás hacia adelante (para {0123456789AB}, R = {BA9876543210}); y la RI consiste en realizar ambas cosas (para {0123456789AB}, RI = {123456789AB0}).
Resumiendo, cuando un compositor elige su material para comenzar a componer una obra dodecafónica, escoge una serie. Y esta serie le proporciona un material compuesto de 48 series que se consideran la misma y que puede utilizar a su antojo: la original, la I, la R, la RI y los transportes de todas ellas. Parece lógico, entonces, dividir entre cuatro la cantidad que nos había quedado de eliminar los transportes (al dividir entre doce en el primer punto). Sin embargo, aquí surge una dificultad: hay ciertas series con características muy peculiares que únicamente tienen una derivada (más los transportes, eso siempre). Me refiero a las series con simetría par y las series con simetría impar.
- En las series con simetría par (como ejemplo, una famosa de Webern: {967845BA2103}), la R coincide con la original (transportada), y la RI coincide con la I. Por lo tanto, únicamente tenemos dos en lugar de cuatro: O (original) e I.
- En las series con simetría impar (como ejemplo, la de antes: {0123456789AB}), la RI coincide con la O, y la R con la I. Por lo tanto, también tenemos dos: O e I.
La dificultad de este problema, radica en contar el número de series con simetría que existen: estas habrá que dividirlas entre dos y el resto entre cuatro. Para esta tarea, vamos a considerar que hemos eliminado todos los transportes dividiendo esos 500 millones entre 12. Daos cuenta de que esto es equivalente a fijar la primera nota a (por ejemplo) {0} y escoger las otras 11.
Series con simetría par
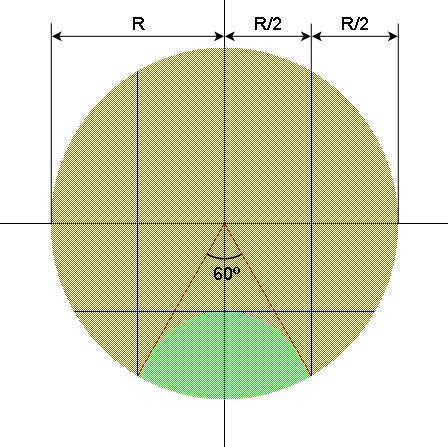
El tritono (diferencia de 6 en nuestro sistema de números) es el único intervalo que al invertirlo se queda igual. Si invertimos {06} nos queda {06} (sumar o restar 6 a {0} nos da siempre {6}). Por lo tanto, una serie tendrá simetría par si y sólo si cada par de notas opuestas (primera y última, segunda y penúltima, etc.) tienen una diferencia de 6. En la escala existen 6 tritonos: {06}, {17}, {28}, {39}, {4A} y {5B}. Así pues, se trata de permutaciones de 5 elementos (recordad que hemos fijado la primera nota a {0}, y por tanto, la última a {6}) y además cada uno de ellos tiene dos posiciones ({17} ó {71}, por ejemplo). Por ello, el número de series con simetría par (sin contar los transportes) es de  .
.
Series con simetría impar
Estas son más complejas. Vamos a ir poniendo notas en la serie de fuera hacia dentro. Tenemos la primera, {0}, y en principio 11 posibilidades para la última. Existen dos casos: que la diferencia entre la primera y última nota sea par o que sea impar. Si la diferencia es par, a la hora de colocar la segunda nota y la penúltima tenemos un problemón: tenemos vetadas dos notas. ¿Por qué? Imaginemos que escogemos {0} y {8} como primera y última nota. Si queremos poner {4} como segunda nota ({0} + 4 = {4}) nos obliga a que la penúltima nota sea {8} — 4 = {4} (!!). Imposible: no se pueden repetir notas. Lo mismo sucede en este ejemplo con la nota {A}. Bien, no hay problema, escogemos otra nota que no sea {4} ni {A}. ¿Qué ocurre entonces? Que pongamos la que pongamos como segunda, nos va a dar una diferencia con la penúltima que va a ser par, luego, a la hora de colocar la tercera nota, nos encontramos con el mismo problema que antes. Si seguimos con el razonamiento, vamos a llegar a la elección de las dos últimas notas y volveremos a tener dos notas vetadas, ¡pero ya no quedan otras!
Conclusión: una serie podrá tener simetría impar si y sólo si la diferencia entre cada par de notas opuestas (primera y última, segunda y penúltima, etc.) es impar. Y es fácil ver que una característica necesaria y suficiente para que se cumpla lo anterior es que la diferencia entre las notas de los extremos sea impar. Volviendo a nuestro planteamiento, si la primera nota es {0}, la última sólo puede ser {1}, {3}, {5}, {7}, {9} ó {B}. 6 opciones. Con dos fijadas, para la segunda nota tenemos 10 posibilidades y, a su vez, fijar esta nota determina la penúltima. Con cuatro fijadas, para la tercera nota tenemos 8 posibilidades… etc. El número total de series con simetría impar (sin contar los transportes) es de  .
.
Y para terminar y hallar esas casi 10 millones de series, realizamos el siguiente cálculo:

Gracias a Tito Eliatron por su ayuda y su paciencia, y enhorabuena al que haya llegado hasta el final de este ladrillo.
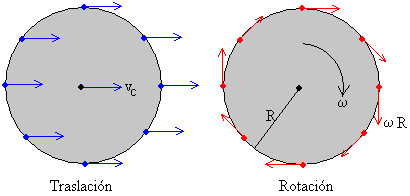
, tenemos que la velocidad angular vale
(que no se asusten los físicos: vamos a meter todos los valores en kilómetros y en horas para no andar haciendo conversiones). La velocidad de rotación en cada punto de la rueda va a ser de
, con
.
y el
respectivamente. A continuación, le sumamos la velocidad de la bicicleta a la componente horizontal y volvemos a hallar el módulo de la velocidad total sumando los cuadrados de las componentes y hallando la raíz cuadrada. Por último, exigimos que este módulo sea menor o igual a 11, la velocidad máxima a la que la fotografía sale nítida. Es decir:
y radio
. Por último, si representamos la expresión de arriba, obtenemos el área coloreada de verde —el esperado círculo— que podemos ver en la imagen inferior.