Problema de nitidez: la solución

A continuación, la solución al problema propuesto ayer. De ahora en adelante, asumiremos que la bicicleta se desplaza por el eje real de izquierda a derecha (de los números negativos a los positivos o, dicho de otra manera, con velocidad positiva) y que captamos la instantánea justo a su paso por el origen. De esta forma, podemos usar el sistema de coordenadas polares con comodidad.

El problema reside en aplicar el principio de superposición de movimientos: por un lado tenemos el movimiento rectilíneo horizontal de la bicicleta, de izquierda a derecha, como hemos comentado; por otro lado, tenemos el giro de la rueda. Esto se denomina movimiento rototraslatorio.

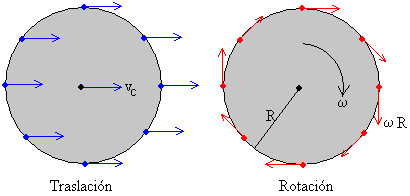
Obviamente, habrá puntos —como se puede intuir a partir de la imagen— en los que la velocidad de rotación se cancelará con la velocidad de traslación y, por ende, saldrán en nuestra fotografía. Para resolverlo, habrá que descomponer la velocidad de rotación de todos los puntos de la rueda en sus componentes vertical y horizontal. Tras esto, a la componente horizontal hay que sumarle la velocidad de traslación y volver a componer el módulo del vector velocidad mediante Pitágoras.

En primer lugar, si la rueda es de radio $R$ , tenemos que la velocidad angular vale $22/R$ (que no se asusten los físicos: vamos a meter todos los valores en kilómetros y en horas para no andar haciendo conversiones). La velocidad de rotación en cada punto de la rueda va a ser de $22r/R$ , con $r\le R$ .

Para hallar las componentes vertical y horizontal de dicha velocidad, es fácil ver que basta con multiplicar por el $-\cos\theta$ y el $\sin\theta$ respectivamente. A continuación, le sumamos la velocidad de la bicicleta a la componente horizontal y volvemos a hallar el módulo de la velocidad total sumando los cuadrados de las componentes y hallando la raíz cuadrada. Por último, exigimos que este módulo sea menor o igual a 11, la velocidad máxima a la que la fotografía sale nítida. Es decir:

$\sqrt{\left(\dfrac{22r}{R}\sin\theta+22\right)^2+\left(-\dfrac{22r}{R}\cos\theta\right)^2}\le11\qquad r\le R$

Si manipulamos esta expresión convenientemente, podemos llegar a lo siguiente:

$r^2-2rR\cos\left(\theta+\dfrac{\pi}{2}\right)+R^2\le\left(\dfrac{R}{2}\right)^2$

Que no es otra cosa que la expresión, en coordenadas polares, de un círculo con centro en $(R,-\pi/2)$ y radio $R/2$ . Por último, si representamos la expresión de arriba, obtenemos el área coloreada de verde —el esperado círculo— que podemos ver en la imagen inferior.

10 comentarios sobre “Problema de nitidez: la solución”

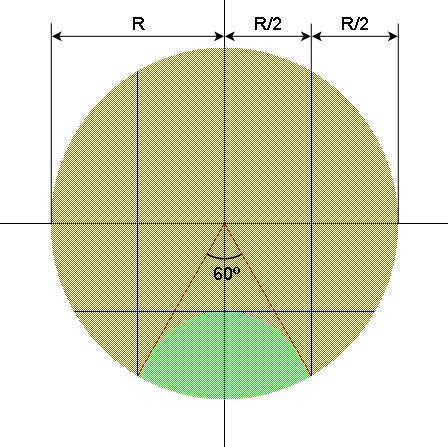
No, si las fórmulas estarán todas bien, pero el chino parece más clarito…

De todos modos, me ha quedado claro en los comentarios del anterior post. Y menos mal. Mi física no alcanza a entender esos garabatos. Usábamos simbología diferente y ya soy muy viejo, o es que nunca llegué a entender nada realmente? Me quedo con la duda ;-)

Lo conseguí resolver poco antes de vértelo, pero me salió mal.

Interesante resultado… ¡sigue así!

Se parece al dibujito que hice ayer. :) Me sorprende la exactitud del ángulo. Que bella es la geometría (más la descriptiva que laa analítica, pero eso es bronca mía)

Pos ayer lo pille con los comentarios, pero con las primeras imagenes ya si que si. Interesante post.

Juas!, y yo que siempre fuí un zote en matemáticas, exactamente como pensaba. Que bien! no tengo que arrancarme ojo izquierdo como pago a mi ignorancia.

Como ya se dijo en los comentarios de ayer, hay una forma más sencilla de llegar a la misma solución: Considerar el eje instantáneo de giro.
El tema consiste en pensar que, para un instante dado, la rueda está girando alrededor de un punto fijo, el del contacto con el suelo, que a su vez tiene velocidad 0. Como la velocidad lineal en el eje de la rueda es de 22, eso significa que la velocidad de rotación en torno al punto de contacto (eje instantáneo de giro) es de 22/R, con lo que la velocidad lineal de cualquier punto es v=22r’/R, siendo r’ la distancia al punto de contacto. Así que todos los puntos que verifiquen que 22r’/R<=11 se verán nítidos, lo que da r'<=R/2, es decir, un círculo con centro el el punto de contacto con el suelo y radio R/2.
Sale lo mismo y nos evitamos la trigonometría y las raíces cuadradas.

Siento mucha pena por no haber estudiado más matemáticas y geometría. También envidia.

Muy interesante.

Que curioso!!!!! La solucion es sorprendente.
Si la camara estuviera en movimiento junto a la bici, ¿verías solo el círculo interior de la rueda de radio menor que R/2?