Aprovechando que mañana se cumple el 40 aniversario de la llegada del hombre a la Luna, os presento esta bellísima aria de Antonín Dvořák, perteneciente a su ópera Rusalka.
Dvořák fue uno de los músicos más representativos del nacionalismo checo, junto con Smetana, de quien hablamos en su día, y Janáček. Probablemente Dvořák sea el más conocido. De hecho, casi todos habréis escuchado alguna vez fragmentos de la célebre Sinfonía del Nuevo Mundo, o las Danzas eslavas, por ejemplo.
Su ópera Rusalka, la novena que escribió, no es menos conocida. Fue estrenada en Praga en 1901 y tuvo un gran éxito entre el público checo (no tanto entre el europeo). Está dividida en tres actos y cuenta una historia que, sin duda, os resultará familiar. La rulsalka, según la tradición eslava era una especie de sirena-fantasma que vivía en el fondo de los ríos. En el libreto de esta ópera, escrito por Jaroslav Kvapil, Rusalka es una ninfa acuática enamorada de un príncipe, que desea hacerse humana para poder estar con él. Para ello acude Jezibaba, la bruja del lago. La bruja atiende la petición de Rusalka, pero a cambio, le arrebata su voz y le advierte de que, si no logra el amor del príncipe, dejará de ser ninfa o humana y estará condenada a vagar en soledad por el lago llevando la muerte a los hombres. Rusalka accede y toma una poción que la convierte en humana.
Cuando el príncipe la encuetra, la lleva a su palacio con la intención de casarse con ella. Sin embargo su mudez lo contraría. Cuando una princesa extranjera llega al palacio, el príncipe se enamora de su hermosa voz y olvida rápidamente a Rusalka. Pronto le declara su amor a la princesa, pero ésta lo rechaza y le dice que siga a Rusalka al infierno.
En este punto la versión de Dvořák se vuelve bastante más macabra que la de Disney (como toda ópera que se precie, ésta no podía tener un final feliz). Rusalka es condenada y, desesperada, le pide ayuda a la bruja Jezibaba. Ésta le indica que debe matar al príncipe, pero ella se niega. A todo esto, el príncipe recuerda su amor por Rusalka y, desolado, la busca sin descanso. Cuando al fin la encuentra, le pide perdón y le ruega que lo bese. Rusalka le advierte que si lo hace, morirá, pero a él no le importa. Por fin se besan y el príncipe muere dichoso.
La Canción a la Luna es un aria perteneciente al primer acto de la ópera. En ella, Rusalka le habla a la Luna de su amor por el príncipe y le pregunta si él la corresponde. Podéis pinchar en el link para leer la letra traducida al castellano. En el vídeo, la soprano Renée Fleming interpreta magistralmente esta aria. A los menos aficionados al canto lírico les recomiendo la versión instrumental a cargo del violinista Joshua Bell.
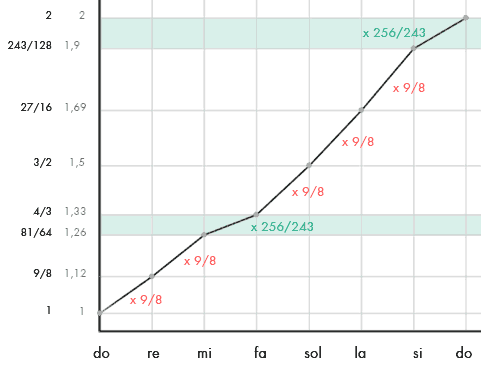
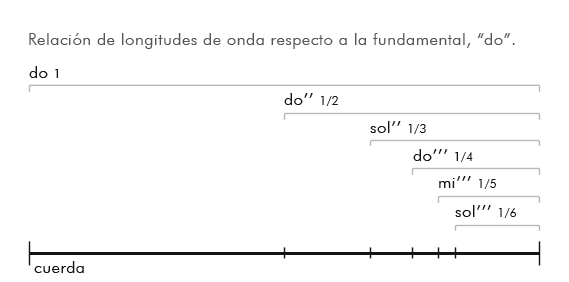
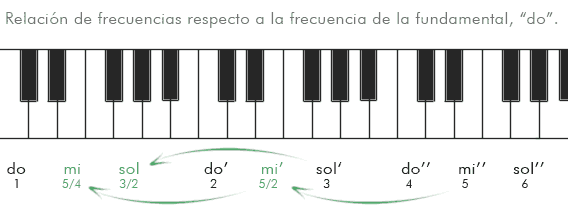
Con estos datos podemos observar varias particularidades de la escala:
