Categoría: Música

A pesar de que el sistema de afinación pitagórico es el único que respecta las dos consonancias principales (8^as y 5^as), la incompatibilidad entre ambas daba lugar a bastantes inconvenientes, tal como vimos la semana pasada. Como alternativa se propusieron otros sistemas a lo largo de la historia, algunos basados en la consonancia de 3ª (como el sistema justo o el mesotónico), otros, en unidades interválicas más pequeñas que el semitono (sistema de Holder, por ejemplo). No tengo especial interés en estos sistemas, pues creo que no aportaron mucho al sistema actual, pero se puede hablar de ellos en otra entrada si alguien tiene interés. Finalmente, el sistema que se impuso fue el sistema temperado, o temperamento igual (en inglés Equal Temperament, ET), basado en 12 semitonos iguales y que sólo respeta la consonancia de 8ª. Todas los demás intervalos, como veremos en esta entrada, resultan ligeramente disonantes. A pesar de ello, es un sistema óptimo para la música tonal, especialmente a partir del Barroco y el Clasicismo: cada vez más llena de modulaciones (cambios de tonalidad o de «escala»), alteraciones accidentales, cromatismos (empleo consecutivo de intervalos de semitono), etcétera.

El semitono temperado:

Es fácil deducir la razón de ser matemática del sistema temperado. Para ello intentaremos averiguar cuánto mide el intervalo de semitono en este sistema. Un intervalo es una proporción de frecuencias, por lo que la frecuencia de cada nota de la escala cromática, se obtendrá de multiplicar la nota anterior por la proporción (razón) correspondiente a un semitono, que por el momento llamaremos «x». Si queremos saber, por ejemplo, cuál es la frecuencia de do#, multiplicaremos la frecuencia de do por «x». Para obtener re, volveremos a multiplicar el resultado obtenido por x, (o la frecuencia de do por x²), etcétera. Por tanto, si queremos completar una 8ª con 12 intervalos iguales, necesitamos un semitono tal que al multiplicarlo 12 veces consecutivas por la frecuencia base, (pongamos 1), dé como resultado una frecuencia doble, (2, el mismo sonido una 8ª más agudo). Esto es: . Por tanto, . Esta es la relación de frecuencias correspondiente a un semitono temperado. Este semitono es intermedio de los pitagóricos: diatónico, , y cromático, .

La escala temperada:

Para hallar la proporción correspondiente a cualquier otro intervalo de la escala temperada, tan sólo tendremos que elevar  al número de semitonos (ST) que contiene dicho intervalo. En la tabla podéis ver una comparativa entre los intervalos pitagóricos, los temperados y los consonantes. Algunas consonancias están entre paréntesis porque son resultado de la inversión de otro intervalo consonante: la 4ªJ es una inversión de la 5ªJ (de do a sol hay una 5ªJ, de sol al do más agudo hay una 4ª), la 3ªm es el intervalo que hay entre mi y sol, ambos consonancias de do, por lo que también suele considerarse consonante, por último, la 6ªM es la inversión de la 3ªm.

También podéis apreciar las diferencias de afinación en este gráfico extraído de la wikipedia, aunque con algunos errores corregidos del original. Los puntos negros son temperados y los azules pitagóricos. El cent es una medida de afinación equivalente a la centésima parte (logarítmica, claro está) de un semitono temperado:

Como podéis ver, ambos sistemas son muy parecidos. Las mayores diferencias se encuentran entre las notas alteradas, especialmente al llegar al sol# (extremo del círculo de 5^as). Sin embargo, si escuchamos la escala diatónica de los sonidos naturales, afinada según el sistema pitagórico o el temperado, resultan casi indistinguibles.

La 5ª Justa:

la 5ªJ temperada es casi idéntica a la pitagórica: difieren aproximadamente 2 cents. Para que os hagáis una idea, podéis escuchar cómo suenan dos sonidos que difieren en 1 cent, 6 ó 10 en esta página de la wikipedia. Son indistinguibles.

La diferencia entre ambas 5^as recibe el nombre de schisma. Para calcular cuánto mide basta dividir la 5ª pitagórica entre la temperada, o bien, repartir la coma pitagórica entre las 12 quintas que cierran el círculo en el sistema temperado. El resultado es el mismo:

La 3ª Mayor.

La 3ªM difiere algo más entre un sistema y otro, pero sigue siendo claramente disonante en ambos. Hasta no oírlo, yo no imaginaba cuanto, así que aquí tenéis el intervalo afinado en ambos sistemas y una 3ªM consonante para compararlos.

Para escuchar más posibles comparaciones, resulta muy útil el programa Scala del que nos habló Zarlino y cuya recomendación yo reitero.

Supongamos una melodía compuesta con las notas de la escala diatónica. Cada nota tendrá una altura (una frecuencia) determinada y, al unir esas alturas, obtendremos el contorno melódico que la caracteriza. Supongamos que esa melodía ha sido compuesta para una soprano, por lo que es bastante aguda. Bien, ahora, imaginemos que tenemos una contraalto, con la voz más grave que Carmen de Mairena, empeñada en cantar esta misma melodía. Tenemos dos opciones: bien dejarla dar gallos para poner a prueba nuestra resistencia a la tortura, o bien, transportar la melodía: es decir, coger su contorno (el patrón de frecuencias característico) y hacer que empiece en una nota más grave.

Esto, en teoría, debería ser bastante fácil. En la antigüedad no se andaban con remilgos y, en lugar de transportar la melodía, transportaban toda la escala sobre la que estaba construida. Así, una nota cualquiera como «do» podía tener una frecuencia de 500 Hz un día, y 635 Hz, al otro. Sin embargo, cuando aparecían en escena instrumentos de afinación fija (como un órgano o un clave), esa aleatoriedad se volvía imposible. Al estar la escala «fija», la única solución era transportar la melodía (hacer que empezase en otra nota de la misma escala) y ahí es donde aparecía el problema: en la escala heptatónica se alternan tonos y semitonos en un orden determinado. Para repetir ese patrón desde otro punto de la escala, es necesario añadir semitonos intermedios entre ciertos tonos (he aquí el origen de las notas alteradas), pero además, es necesario que todos estos semitonos sean iguales, lo que no sucede en el sistema pitagórico.

En música, existen dos tipos de notas alteradas: los bemoles (♭), que son notas «bajadas» medio tono, y los sostenidos (#), notas «subidas» medio tono. Si todos los semitonos fuesen iguales, un do# debería sonar igual que un re♭, un re# igual que un mi♭, etcétera. Estas parejas de notas a las que les corresponde el mismo sonido se denominan enarmonías. Para que sean posibles, el sonido de cada alteración debe ser intermedio de las dos notas naturales adyacentes, pero, debido a la imperfección del círculo de 5^as, en el sistema pitagórico, los bemoles se aproximan más a la nota inferior y los sostenidos, a la superior. En esta entrada veremos por qué.

La quinta del lobo

Hace dos entradas, hablamos del origen de la escala heptatónica. Bastaba con enlazar varias quintas empezando por el fa y terminando en el si. Bien, más allá del fa y del si, para medir los intervalos de 5ª, no nos bastará con contar cuántas notas separan los extremos. Si así lo hiciésemos, al contar 5 notas ascendentes desde el si, volveríamos a obtener un fa y viceversa. Sin embargo, esta quinta es más pequeña de lo normal: sólo tiene 6 semitonos, mientras que las demás tienen 7. Por ello recibe el nombre de 5ª disminuida. El sistema pitagórico se basa en la 5ªJusta de 7 semitonos (podemos observar que el sistema es coherente: con 12 quintas de 7 semitonos, igualamos 7 octavas de 12 semitonos). Así, para subir una 5ªJ desde el si, tendremos que llegar hasta el fa# y, para bajar una desde el fa, usaremos el si♭.

Recordemos ahora que 12 quintas bien afinadas son un poquito más de 7 octavas. Si queremos cerrar el círculo en este punto, una de las quintas tendrá que medir un poquito menos que el resto (una coma pitagórica menos), no será perfectamente consonante y sonará bastante mal. Por ello, era conocida como quinta del lobo y se procuró situarla entre dos sonidos que no se empleasen habitualmente, lo más alejados posible de la escala natural. El oscuro rincón elegido fue entre el el sol# y el mi♭ que se tomaron como los extremos del círculo de quintas. Así, para afinar los semitonos entre el la-si y el re-mi, se optó por descender dos quintas a partir del fa natural, obteniendo así si♭ y mi♭. Los sonidos fa#, sol# y do# se consiguen al subir 3 quintas desde el si.

Esto significaba que, en los instrumentos de afinación fija que utilizaban este sistema, el la♭, (, afinado como un sol#, ), o el re#, (, afinado como un mi♭, ), podían sonar bastante mal, por lo que no convenía alejarse mucho de las tonalidades más cercanas a la escala natural. Podéis apreciarlo en la espiral logarítmica de la semana pasada.

Semitonos cromáticos y diatónicos

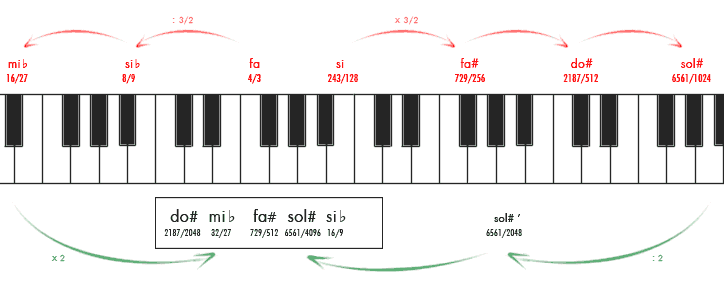
En este gráfico tenéis la misma espiral con las frecuencias de la escala cromática, pero esta vez, dado que cada 360º se repite el mismo sonido, he unido cada nota con el origen. Así, podemos ver todos los sonidos en una misma octava y observar más fácilmente los ángulos que las separan (representativos de los intervalos correspondientes). Aunque pueda parecerlo, los 12 ángulos de la imagen (12 semitonos), no son exactamente iguales: hay cinco de mayor tamaño (semitonos cromáticos) y 7 más pequeños (diatónicos).

Los semitonos cromáticos son los que hay entre notas con el mismo nombre, una natural y otra alterada, esto es, entre: do-do#, mi♭-mi, fa-fa#, sol-sol# y si♭-si. Todas estas notas se hayan en proporción de . En la imagen podéis apreciar que los ángulos son claramente mayores que los correspondientes a los semitonos diatónicos (semitonos entre notas con distinto nombre): do#-re, re-mi♭, mi-fa, fa#-sol, sol#-la, la-si♭ y si-do. La proporción en este caso es de . La diferencia, de nuevo, no es mucha: exactamente de una coma pitagórica:

Todo esto los violinistas lo saben bien, pues, a pesar de que este sistema de afinación ya no se utiliza, suele sonar mejor una nota sostenida (como fa#, sensible) que resuelve ascendentemente (sol), si ambos sonidos  están más próximos, como separados por un semitono diatónico. Por eso, quizás lleguéis a escucharles decir que las enarmonías no son posibles, que un sol♭ no es lo mismo que un fa# y demás, pero siempre en boca de la cuerda frotada: un pianista se partiría el culo.

Por último, podéis comprobar por qué la 5ª del lobo es más pequeña que el resto: mientras todas las demás tienen 3 semitonos cromáticos y 4 diatónicos, el intervalo entre mi♭ y sol#, tiene 2 semitonos cromáticos y 5 diatónicos. La diferencia es, por tanto, la prevista: una coma pitagórica.

Nota para músicos

Supongo que muchos ya habréis caído en la cuenta al leer estas entradas: el origen de la escala heptatónica explica también el orden de las tonalidades y de las alteraciones en la armadura de clave. Sol Mayor, por ejemplo, necesita solo un sostenido, pues al estar una 5ª por encima de do, utiliza los mismos intervalos para construir su escala y únicamente «se sale» de los sonidos naturales en la última 5ª,  de si a fa#.