(Esta anotación se publica simultáneamente en Naukas)
Supongamos que queremos diseñar un experimento para medir la aceleración de la gravedad. Disponemos de unas herramientas matemáticas —las ecuaciones del movimiento— que describen cómo se mueve un cuerpo en función de diversos parámetros, entre ellos, la aceleración a la que está sometido. Disponemos también de unas herramientas experimentales para diseñar el dispositivo de experimentación y medida, cuyo propósito será tomar datos con los que alimentar nuestras ecuaciones y obtener la incógnita buscada.
Muy probablemente, dicho experimento consistirá en dejar caer uno o varios objetos desde diversas alturas tabuladas y medir los tiempos de caída. Estaremos de acuerdo en que, dada una altura, un objeto tardará en caer cierto tiempo, siempre el mismo. No obstante, creo que nadie se sorprenderá a estas alturas si digo que generalmente no hay dos medidas que salgan iguales. La razón es que en la vida real tenemos que lidiar con el error. En la realidad, nada dura cinco segundos, sino cinco más/menos algo que hay que cuantificar. La realidad es caótica y el control de las condiciones experimentales para reducir y al mismo tiempo cuantificar ese algo, ese error, es una de las tareas más arduas que existen. Cualquiera que haya pisado un laboratorio lo entenderá, máxime si trabaja con cosas muy pequeñas o cosas vivas.
Pero volvamos a nuestro experimento. Tenemos que tener claro desde el principio que toda medida que realicemos va a tener un error asociado que categorizamos en dos tipos: error sistemático y error aleatorio. El error sistemático determina lo que denominamos exactitud, ya que afecta a todas las medidas de la misma forma. En nuestro ejemplo, podría haber diversas fuentes de error sistemático como, por ejemplo, errores de calibración en los instrumentos de medida que hicieran que midamos siempre alturas más cortas o más largas, o tiempos más cortos o más largos. Idealmente, un análisis pormenorizado dará con todas las fuentes de error sistemático y las eliminará, pero, en último término, tiene la ventaja de que se puede identificar y medir a posteriori para eliminarlo de un plumazo de todos los datos ya recogidos. Por ejemplo, nos damos cuenta de que el cronómetro estaba tardando un segundo en pararse desde que le dábamos al botón; entonces, basta con restar un segundo a todas las medidas.
El error aleatorio, por su parte, afecta a la precisión y, en principio, parece mucho más escurridizo. Tiene que ver con desviaciones aleatorias que se producen alrededor de cierto valor que es el que queremos determinar, ese tiempo ideal que nuestra teoría muestra que tarda cualquier objeto en caer desde tantos metros de altura. Por ejemplo, más o menos se ve que el objeto cae en cinco segundos desde cierta altura, pero a veces medimos cinco y un poquito y otras, cinco menos un poquito. La solución que se suele adoptar es realizar muchas medidas en una misma configuración (misma altura, mismo objeto) y hacer la media de todas. Pero ¿por qué la media? ¿Es esto correcto?
Bien. A primera vista, nada nos garantiza que la distribución de las desviaciones alrededor de ese valor real sea simétrica. Nada impide que cierta fuente de error aleatorio tenga esta pinta:
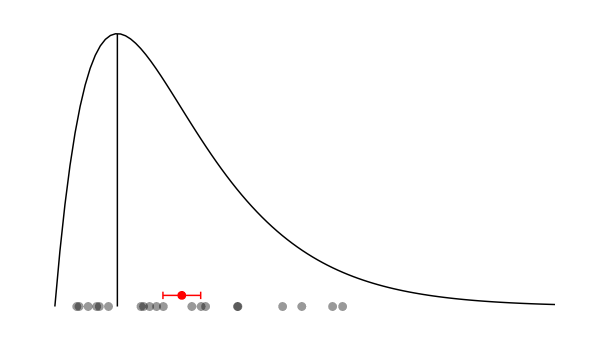
La línea vertical representa el valor real que queremos obtener. La montaña representa la distribución de las desviaciones debidas a ese hipotética fuente de error. Abajo, hay 20 puntos grises correspondientes a 20 medidas diferentes en una misma configuración experimental. En rojo, la media de esas medidas con su error asociado. ¡Vaya! ¡Fallamos! ¿Qué estamos haciendo mal?
En la realidad, suceden dos cosas que nos vienen muy bien. Por un lado, no es común encontrar una fuente de error aleatorio que se comporte de forma asimétrica —aunque haberlas, las habrá—. Por otro lado, nunca hay una única fuente de error aleatorio, y esto es importante: el error aleatorio estará compuesto por múltiples fuentes (y de muchas no seremos ni conscientes). Y ahora, nos da igual cómo sea cada fuente de error; incluso nos da igual que haya fuentes asimétricas… Las matemáticas vienen a socorrernos en forma de lo que se denomina Teorema Central del Límite (TCL). Dicho teorema demuestra que, dadas las condiciones que estamos describiendo (múltiples fuentes de error independientes), la distribución del error aleatorio total sigue una distribución normal —una campana de Gauss de toda la vida—. ¿Y cuál es el parámetro por excelencia de dicha distribución? Exacto: la media. Veamos:
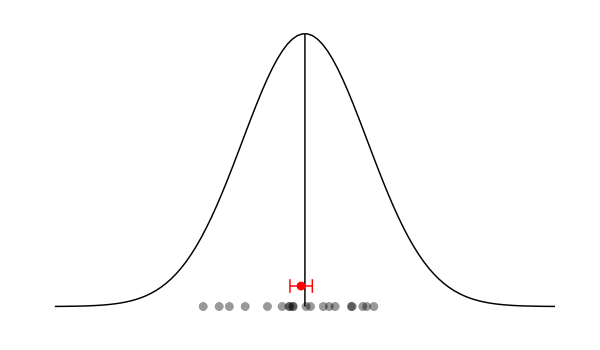
Otras 20 medidas bajo este nuevo supuesto y nuestra media lo clava (dentro del error, coletilla imprescindible).
Existe una frase célebre de Gabriel Lippman en una discusión con J. H. Poincaré acerca del TCL que reza así, no sin falta de sorna:
Los experimentalistas piensan que es una verdad matemática mientras los matemáticos creen que es un hecho experimental.
Ahora sabemos que es la combinación de ambos: se trata de una verdad matemática construida sobre unas condiciones que se dan de hecho en la experimentación. Sir Francis Galton, ya en 1889, le dedicó las siguientes palabras:
Conozco pocas cosas tan propensas a golpear la imaginación como esta maravillosa forma de orden cósmico expresada por [el Teorema Central del Límite]. Esta ley habría sido personificada por los griegos y deificada si la hubieran conocido. Reina con serenidad y completa humildad en medio de la más salvaje confusión. Cuanto más grande es el desorden, la aparente anarquía, más perfecto es su influjo. Es la ley suprema de la Sinrazón. Cada vez que una gran muestra de elementos caóticos es examinada y alineada en su orden de magnitud, una insospechada y bellísima forma de regularidad demuestra haber estado siempre ahí, latente.