La demostración del Teorema de Pitágoras

Publicado el por Iñaki Úcar

Se trata de una demostración sencilla y elegante ideada por Einstein con tan sólo 11 años. Lo vio Pseudópodo en el libro Fractals, Chaos, Power Laws, de Manfred Schroeder, y lo explica de manera magnífica en su blog, así que no cambiaré ni una coma:

Esta es la demostración más sencilla y elegante que existe (y que puede existir, creo yo) del Teorema de Pitágoras.

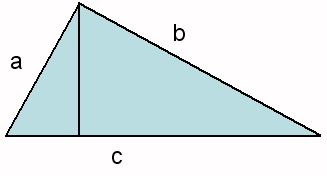
En el triángulo original, de lados a,b,c, trazamos una altura. Se forman así dos nuevos triángulos rectángulos. El de la izquierda tiene por hipotenusa a; llamaremos a su área Sa; el de la derecha tiene por hipotenusa b, y su área será Sb. El triángulo original, con hipotenusa c, tendrá un área Sc.

Estos tres triángulos son semejantes porque tienen ángulos iguales. En el plano euclídeo, el área de cualquier figura geométrica es proporcional al cuadrado de su dimensión lineal. Podemos escribir por tanto que:

Sa = k·a2
Sb = k·b2
Sc = k·c2

donde k es una constante igual en las tres ecuaciones (ya que los triángulos, al ser semejantes, son la misma figura geométrica).

Además, es obvio que

Sc = Sa + Sb

Sustituyendo aquí las ecuaciones anteriores,

c2 = a2 + b2

Limpio, claro e indoloro. ;-)

17 comentarios sobre “La demostración del Teorema de Pitágoras”

  2. Desde luego alcanza esa simpleza tan buscada en las matemáticas, si se redujera un poco y cupiese en una camiseta; sería uno de los regalos de esta navidad.

  4. Esta prueba en realidad data de mucho más anterior a Einstein. La versión más antigua que se tiene de esta prueba es alrededor de 1150 por el matemático y astrónomo hindú Bhaskara (quien además de esta prueba dio otra prueba por disección (la que rotuló como «¡mirad!»).

    Además esta misma prueba fue redescubierta por John Wallis (matemático inglés) en el siglo XVII.

    Precisamente por su simplicidad, esta prueba ha sido «descubierta» muchas veces en la historia, Einstein no el primero ni el último.

    Notar también que Bahksara es hindú, por lo que quizás el hecho de que los hindús eran más «aritméticos» que los griegos (geométricos) esté relacionado con que esta prueba no es una de las pruebas griegas «clásicas» (la de Pitágoras por disección, la de Euclides por áreas)

    — drini

  7. hhhhhhhhhhhhhhhhoooooooooooooooooollllllllllaa

    bbbbbbbbbbbbbbbbbbyyyyyyyyyyyyyyeeeeeeeeeeeee

  9. luis, tenías que ser subnormal. Aprende a escribir y a curarte los prejuicios. Tú mismo, con tu frase, eres la prueba viviente de que los retrasos mentales no dependen del aparato reproductor de quien los sufre: todo está en tu mente, exclusivamente.

  13. MUY BIEN ESPLICADO,GRACIAS POR COMPANTIR DOS DE LAS COSAS MAS PERSONALES Y VALIOSAS COMO SON EL CONOCIMIENTO Y EL TIEMPO.

  14. esto me parese muy bien es muy interesante para las personas que estudiamos en alguna institucio
    bueno
    bbbbbbbbyyyyyyyyyeeeeeeeeee………..

  15. me podrias explicar bien que significa: » En el plano eu­clí­deo, el área de cual­quier fi­gu­ra geo­mé­tri­ca es pro­por­cio­nal al cua­dra­do de su di­men­sión li­neal «. Asi comprendo bien la justificacion para el teorema, gracias.

    si puedes, respondeme a mi mail asi tengo la respuesta alli

  16. @sergio: Significa que, cuando escalamos una figura geométrica en un factor x, sus longitudes se ven multiplicadas por x mientras que las áreas se multiplican por x2.

Comentarios cerrados.